概率论和数理统计

分布律

$$P=\{X=x_k\}=p_k$$

此为离散型随机变量X的分布律

分布函数

离散型

$$F(x)=P(X<=x)$$

连续型

$$F(x)=\int_{-\infin}^x f(t)dt$$

函数F为X的分布函数，$f(x)$叫概率密度函数

方差

方差定义：

• $D(X)=E\{[X-E(X)]^2\}$

方差即为对函数$g(X)=(X-E(X))^2$的数学期望，即X到均值附近的分布情况

离散型

$$D(X)=\sum_{k=1}^\infin [x_k-E(X)]^2p_k$$

其中$P\{X=x_k\}=p_k$是X的分布律

连续型

$$D(X)=\int_{-\infin}^\infin[X-E(X)]^2f(x)dx$$

其中$f(x)$是概率密度

随机变量X的方差可以按照下列公式计算

$$D(X)=E(X^2)-[E(X)]^2$$

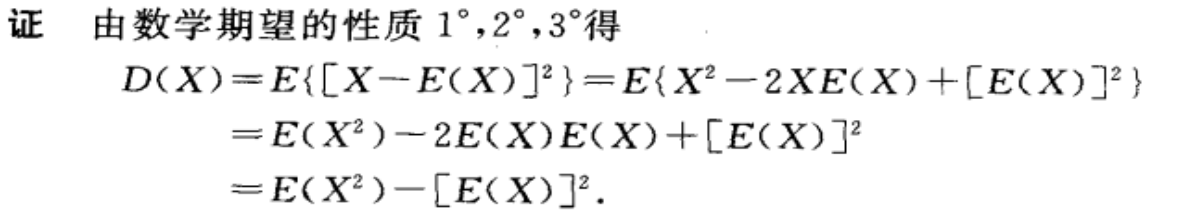
协方差

矩、协方差矩阵

协方差矩阵

称为随机变量$(X_1, X_2)$的协方差矩阵

中心极限定理

联合分布率

$P\{X=x_i,Y=y_j\}=p_{ij}$为二维离散随机变量XY的分布律，或者随机变量X和Y的联合分布律

样本分位数 p64

常用统计量的分布 p138

点估计

估计值为估计。

案例

两个构造估计量的方法

最大似然估计

按照事情已经发生的情况去求把似然函数写出来，即发生现在的情况的函数，让他的概率最大！