梯度更新
Kong Liangqian Lv6
 2022-05-07 18:38:29  

负梯度方向说明

民见传闻，当我们寻找凸函数最小值的时候，沿着负梯度方向去寻找是可以找到最小值的，为何？

假设有一个函数$y=f(x)$， 他存在着最小值$f(x_0)$， 假设我们移动一小步$\Delta x$

很明显，当$\Delta x = -f’(x)$的时候，$f(x+\Delta x) - f(x)=- f’(x)^2 < 0$，当取负梯度方向的时候，可以保证下一步的取值肯定小于这一次的。

迭代可视化示例

给定一个函数

$x$轴有两个方向，需要对两个方向分别求偏导数

给定一个初始值$x_0=(x_{10}, x_{20})$, 后续按照负梯度方向更新

这里, $\eta$为步长

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
# 导入相关库
import math
import random
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from tqdm.notebook import tqdm
from mpl_toolkits.mplot3d import Axes3D

# 定义一个二元函数
def func_1(x1, x2):
	return 3*x1*x1 + 2*x1*x2 + 6*x2*x2



# 对照原函数求偏导数
def hx1(x1, x2):
    return 6*x1 + 2*x2

def hx2(x1, x2):
    return 12*x2 + 2*x1


# 定义初始值、学习率以及迭代次数（可以换成随机数试试哦）
x1 = 5 # random.uniform(-5, 5)
x2 = 5 # random.uniform(-5, 5)
Lr = 0.05
Epochs = 100

# 保存梯度下降经过的点
GD_X1 = [x1]
GD_X2 = [x2]
GD_Y = [func_1(x1,x2)]


for epoch in tqdm(range(Epochs)):
    tmp_x1 = x1 - Lr * hx1(x1,x2)
    tmp_x2 = x2 - Lr * hx2(x1,x2)
    tmp_y = func_1(tmp_x1,tmp_x2)
    
    x1 = tmp_x1
    x2 = tmp_x2
    
    GD_X1.append(x1)
    GD_X2.append(x2)
    GD_Y.append(tmp_y)

print("最终结果为:(x1:%.5f, x2:%.5f, 最值：%.5f)" % (x1, x2, func_1(x1,x2)))


X1 = np.arange(-5, 5)
X2 = np.arange(-5, 5)
X1, X2 = np.meshgrid(X1, X2)
Y = np.array(list(map(lambda t : func_1(t[0],t[1]),zip(X1.flatten(),X2.flatten()))))
Y.shape = X1.shape
fig = plt.figure(facecolor='w', figsize=(20,18))
ax = Axes3D(fig)

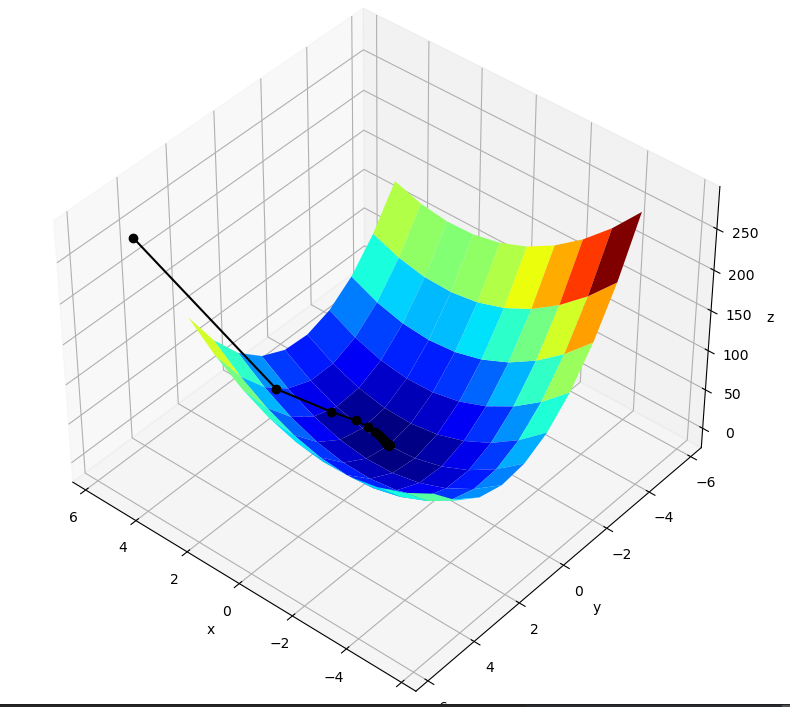
ax.plot_surface(X1, X2, Y, rstride=1, cstride=1, cmap=plt.cm.jet, zorder=0)
ax.plot3D(GD_X1, GD_X2, GD_Y, 'ko-', zorder=10)

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('Func;\nLr:%.3f; Final result:(%.3f, %.3f, %.3f)' % (Lr, x1, x2, func_1(x1,x2)))
plt.show()

 Comments